浅述底池权益实现

为了充分理解底池权益实现（Equity Realization），我们首先需要仔细理解Equity这个概念。不幸的是，Equity这个术语往往被用于指代两个不同的概念。有时它指代我们的牌获胜的可能性（胜率），有时它指代我们的底池份额（底池权益）。我们现在给这不同两个概念更明确的名称，以便区分它们：

Hand Eqity（HE，底牌胜率）＝我们的牌获胜的可能性（我们的胜率）

Pot Equity（PE，底池权益）＝我们的底池份额

注意，当我们讨论底牌胜率时，我们通常是做一个估算。这是Equilab这样的扑克工具可以派上用场的地方。我们可以输入我们的底牌和对于对手范围的最好猜测，工具将为我们计算出百分比胜率。

当然，这只是一个估算，因为假设还有筹码剩余，某个牌手可能决定在后续回合弃牌（即可能产生弃牌赢率）。这就是底池权益实现发挥作用的地方。

在扑克中，底池权益实现被用来描述我们的预估底牌胜率和我们真实底牌胜率之间的关系。它也可能用来描述我们的评估价值和我们的实际价值之间的关系。虽然诸如牌手水平差异这样的因素难以量化，但其他因素（比如位置、筹码深度、可玩性）比较容易量化，特别是我们使用GTO工具的时候。

我们来看一个我们在盲注0.5/1美元的牌局面对翻牌圈决定的例子。

我们坐在小盲位置，前面玩家都弃牌，我们的底牌是3♥ 3♠。

我们和大盲玩家都有100美元筹码。我们加注到3美元，然后大盲玩家跟注。

翻牌是T♠ 7♦ 2♥。

如果我们假定大盲玩家用一个50%起手牌的范围跟注，那么Equilab得出的结果是：

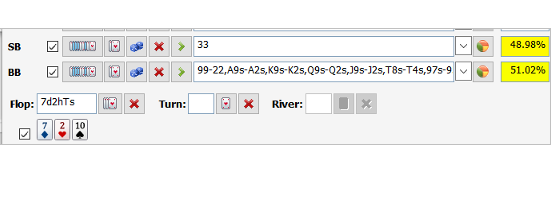
完整的大盲位置范围是：{99-22, A9s-A2s, K9s-K2s, Q9s-Q2s, J9s-J2s, T8s-T4s, 97s-95s, 86s-85s, 75s-74s, 64s, 53s, 42s+, 32s, AJo-A2o, K6o+, Q7o+, J7o+, T7o+, 97o+, 87o, 76o, 65o, 54o}

我们的预估底牌胜率是49%。

如果没有更多下注进入底池（比如两个牌手都一直check到河牌圈），那么我们的EV将是：

EV = 底池 x 底牌胜率 = 6 x 0.49 = 2.94（美元）

如果我们把同样的底牌输入到PIOSolver这样的GTO工具会怎样？我们可以得出一个EV的更真实价值，因为工具把位置、筹码深度和底牌可玩性这些因素也考虑进来了。给下注尺度做一些假定后，PIOSolver展示给我们的EV是：

现在我们可以对我们的底池权益实现（或R）做一个更精确的量化陈述：

R = 真实EV / 预估EV = 1.36 / 2.49 = 0.55

因此，我们可以看出，由于处在不利位置，筹码底池比较高，一手可性差的底牌只能产生我们最初预计价值的55%。

为了培养你的意识，使你知道这些因素将如何影响你的不同底牌在不同公共牌面的底池权益实现，用扑克工具做这样的计算作为一种良好的练习。当你开始用这些GTO工具运行翻牌面子集时（flop subsets），情况变得真正有趣起来。翻牌面子集是用少数仔细选择的翻牌面来代表所有可能翻牌面的一种尝试。这种方法的好处是，通过简化整个翻牌面集合，普通的家用电脑能够得出我们的范围翻前对抗另一个范围绩效如何的一些有意义的结论。了解这些知识后，你可以计算一手单独底牌对抗给定范围的底池权益实现（R）。这也意味着你可以判断任何给定底牌是否值得翻前率先加注。

这就是底池权益实现的强大!

扑克反水-德州扑克反水-博狗扑克反水-蜗牛扑克反水-扑克之星反水-联众扑克反水-天龙扑克反水